Bubble sorting is the most popular sorting technique because it is very simple to understand and implement. The algorithm achieves its name from the fact that with each iteration the largest value moves like a bubble to the top of the array. The bubble sort method is not efficient for large arrays.
Bubble Sort Algorithm
The bubble sort work as follows:
If N (no. of elements)elements are given in memory then for sorting we do the following steps:
- First, compare the 1st and 2nd elements of the array. If 1st<2nd, then no interchange else interchange 1st and 2nd elements.
2. Now compare 2nd and 3rd. If 2nd >3rd then interchange the value of 2nd and 3rd. Otherwise no interchange.
3. Now compare the 3rd with 4th elements, if 3rd>4th then interchange the value of 3rd and 4th, otherwise no interchange.
4. Similarly compare until N-1TH elements are compared with Nth elements.
5. At the end, the highest element value is reached at the Nth place.
6. Now elements will be compared until N-1 passes.
In every pass, one element is reached at the end. So, if a number of elements is in N, then it takes N-1 passes to sort the N elements. Let us take elements 28,20,30,15 and 05 ends illustrate the same. Here N=5,
A[5]
A[0]=28;
A[1]=20;
A[2]=30;
A[3]=15;
A[4]=05;
Pass 1:
The comparison for pass1 is as follows.
Compare A[0] and A[1]. Since 28>20, interchange them.
Compare A[1] and A[2]. since 28<30, no change.
Compare A[2] and A[3]. Since 30>15 interchanges them.
Compare A[3] and A[4]. Since 30>05, interchange them.
At the end of the first pass, the largest element of array 30 is bubbled up to the last position in the array
The answer is ……….A[5];
A[0]=20;
A[1]=28;
A[2]=15;
A[3]=05;
A[4]=30; //largest element
Pass 2:
The comparison for pass2 is as follows:
Compare A[0] and A[1]. Since 20<28, no change
Compare A[1] and A[2]. since 28>15, interchange them
Compare A[2] and A[3]. Since 28>05 interchange them.
The answer is………….A[5];
A[0]=20;
A[1]=15;
A[2]=05;
A[3]=28; //second largest
A[4]=30; //largest element
At the end of pass2, the second largest element of the array, 28 is bubbled up to the 3rd position in the array.
Pass 3:
The comparison for pass3 is as follows.
Compare A[0] and A[1]. Since 20>15, no change
Compare A[1] and A[2]. since 20>05, interchange them
The answer is……A[5];
A[0]=15;
A[1]=05;
A[2]=20; //third largest
A[3]=28; //second largest
A[4]=30; //largest element
At the end of 3rd pass, the third largest element 20 is bubbled up to the 2nd position in the array.
Pass 4:
The comparison for pass4 is as follows.
Compare A[0] and A[1]. Since 15>05, interchange them
Answer……..A[5];
SORTED ARRAY
A[0]=05;
A[1]=15;
A[2]=20; //third largest
A[3]=28; //second largest
A[4]=30; //largest element
If the number of elements is 5, then at the end of the 4th pass the array elements are in sorted order. In every pass, the number of comparisons is decremented. i.e.,
1st pass …4 comparison
2nd pass…3 comparison
3rd pass…2 comparison
4th pass…1 comparison.
For(j=0;j<=n-pass-1;j++)
{
If(a[j]>a[j+1])
{
Temp=a[j];
A[j]=a[j]+1;
A[j+1]=temp;
}
}
When pass=1, j ranges from 0 to (5-1-1) i.e. 0 to 3. So 4 comparisons take place
When pass=2, j ranges from 0 to (5-2-1)i.e, 0 to 2. So 3 comparisons take place
When pass=3 j ranges from 0 to (5-3-1)i.e , 0 to 1. So 2 comparisons take place
When pass=4 j ranges from 0 to (5-4-1)i.e, 0 to 0 .So 1 comparison takes place
As the value of the pass is varying from 1 to (n-1), the value of comparisons from (n-1) to 1 respectively.
//Program to sort ‘n’ number using Bubble Sort
#include<stdio.h>
#include<conio.h>
void bubble_sort(int [],int);
void main()
{
int i,j,a[20],n,temp;
clrscr();
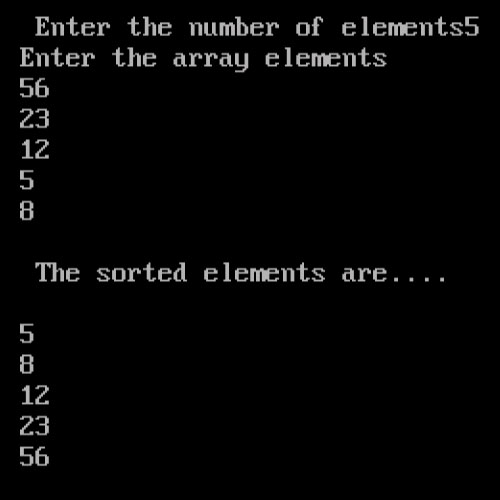
printf(“\n Enter the number of elements”);
scanf(“%d”,&n);
printf(“Enter the array elements”);
for(i=0;i<n;i++)
scanf(“%d”,&a[i]);
bubble_sort(a,n); //calling function
printf(“\n The sorted elements are….\n”);
for(i=0;i<n;i++)
printf(“%d”a[i]);
getch();
}
//Function to sort n elements using Bubble Sort
void bubble_sort(int a[],int n)
{
int pass,temp,j;
for(pass=1;pass<n;pass++)
{
for(j=0;j<=n-pass-1;j++)
{
if(a[j]>a[j+1])
{
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
}
//Bubble Sort Program in Data Structure
/*Program of sorting using bubble sort */
#include <stdio.h>
#define MX 20
void main()
{
int arr[MX],ii,jj,k,temp,lnum,exchanges;
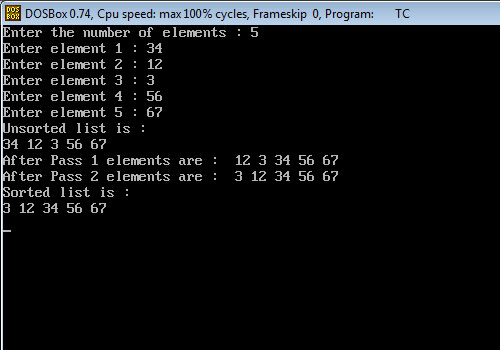
printf(“Enter the number of elements : “);
scanf(“%d”,&lnum);
for (ii = 0; ii < lnum; ii++)
{
printf(“Enter element %d : “,ii+1);
scanf(“%d”,&arr[ii]);
}
printf(“Unsorted list is :\n”);
for (ii = 0; ii < lnum; ii++)
printf(“%d “, arr[ii]);
printf(“\n”);
/* Bubble sort*/
for (ii = 0; ii < lnum-1 ; ii++)
{
exchanges=0;
for (jj = 0; jj <lnum-1-ii; jj++)
{
if (arr[jj] > arr[jj+1])
{
temp = arr[jj];
arr[jj] = arr[jj+1];
arr[jj+1] = temp;
exchanges++;
}/*End of if*/
}/*End of inner for loop*/
if(exchanges==0) /*If list is sorted*/
break;
printf(“After Pass %d elements are : “,ii+1);
for (k = 0; k < lnum; k++)
printf(“%d “, arr[k]);
printf(“\n”);
}/*End of outer for loop*/
printf(“Sorted list is :\n”);
for (ii = 0; ii < lnum; ii++)
printf(“%d “, arr[ii]);
printf(“\n”);
}/*End of main()*/
Efficiency:
In bubble sort, n-1 comparisons are made in pass1, n-2 in pass2, n-3 in pass3, and so on. Let F(n) be the complexity function.
Total number of comparisons=F(n)=(n-1)+(n-2)+(n-3)+………+3+2+1.
It is in the form of arithmetic progression series. So we can apply the formula
Sn=n/2[2a+(n-1)d]
Where n=number of elements in a series.Here it is(n-1).
a=first element in series. Here it is 1.
d=difference between the second element and the first element. Here it is 1.
Sn =(n-1)/2[2*1+(n-1-1)*1]
=(n-1)/2[2+n-2]
=n(n-1)/2
Where is of 0(n2).

