Introduction to Recursion in Data Structures
Recursion in data structure is a process where a function calls itself to solve smaller instances of the same problem until it reaches a base case, which stops the recursion. Recursion in data structure is a fundamental concept used in programming and data structures to solve complex problems in a simpler, more modular way. Recursion in data structure (self-referential approach) is well-suited for problems with repetitive, nested, or hierarchical structures, such as trees, graphs, and linked lists.
Key Concepts of Recursion in Data Stucture
- Base Case: A condition that terminates the recursion to prevent infinite calls.
- Recursive Case: The part where the function calls itself with a smaller(module) problem
int factorial(int no)
{
if (no == 0) // Base Case
return 1;
return n * factorial(no – 1); // Recursive Case
}
Stack Mechanism
- Every recursive call is stored on the call stack, along with its local variables and return address.
- The stack follows LIFO (Last In, First Out).
- Recursive functions are memory-intensive due to stack usage.
Types of Recursion in Data Structure
Direct Recursion:
Function calls itself directly.
void directRecursion()
{
// Function(directRecursion()) directly calls itself
directRecursion();
}
Indirect Recursion:
The function calls another function(functionB()), which calls the original function.
void functionA() {
functionB();
}
void functionB() {
functionA();
}
Why Use Recursion in Data Structures?
- Hierarchical Structures: Recursion mirrors the hierarchical nature of data structures like trees and graphs.
- Simplified Code: Many algorithms for traversing or manipulating data structures can be more concise and intuitive with recursion.
- Divide and Conquer: It is a natural fit for algorithms that divide problems into smaller subproblems, such as Merge Sort or Quick Sort.
Advantages of Recursion in Data Structure
- Elegant and concise solutions for complex problems.
- Intuitive handling of hierarchical or nested data structures.
- Avoids explicit stack or iterative code for certain problems.
Disadvantages of Recursion in Data Structure
- Stack Memory Usage: Each recursive call adds a frame to the call stack, which can lead to a stack overflow for deep recursions..
- Performance overhead because of repeated function calls.
- Risk of stack overflow if the recursion depth is too large or not controlled.
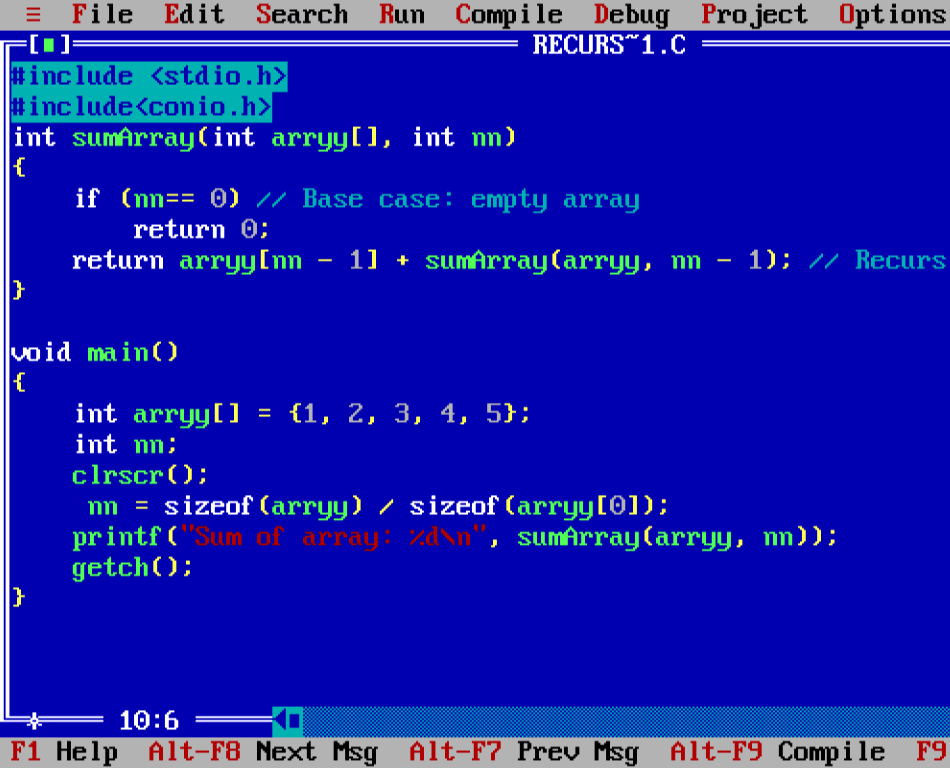
1. Recursion in Arrays
Example: Sum of Array Elements
#include <stdio.h>
#include<conio.h>
int sumArray(int arryy[], int nn)
{
if (nn== 0) // Base case: empty array
return 0;
return arryy[nn – 1] + sumArray(arryy, nn – 1); // Recursive case
}
void main()
{
int arryy[] = {1, 2, 3, 4, 5};
int nn;
clrscr();
nn = sizeof(arryy) / sizeof(arryy[0]);
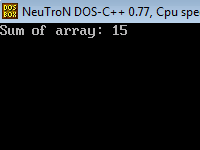
printf(“Sum of array: %d\n”, sumArray(arryy, nn));
getch();
}
Examples in Data Structures
- Arrays: Operations like summing elements, finding the maximum, or reversing.
- Linked Lists: Traversal, reversing, or searching for an element.
- Trees: Traversals like pre-order, in-order, post-order, or finding the height.
- Graphs: Depth-first search (DFS).
- Divide and Conquer Algorithms: Sorting algorithms like Merge Sort and Quick Sort.
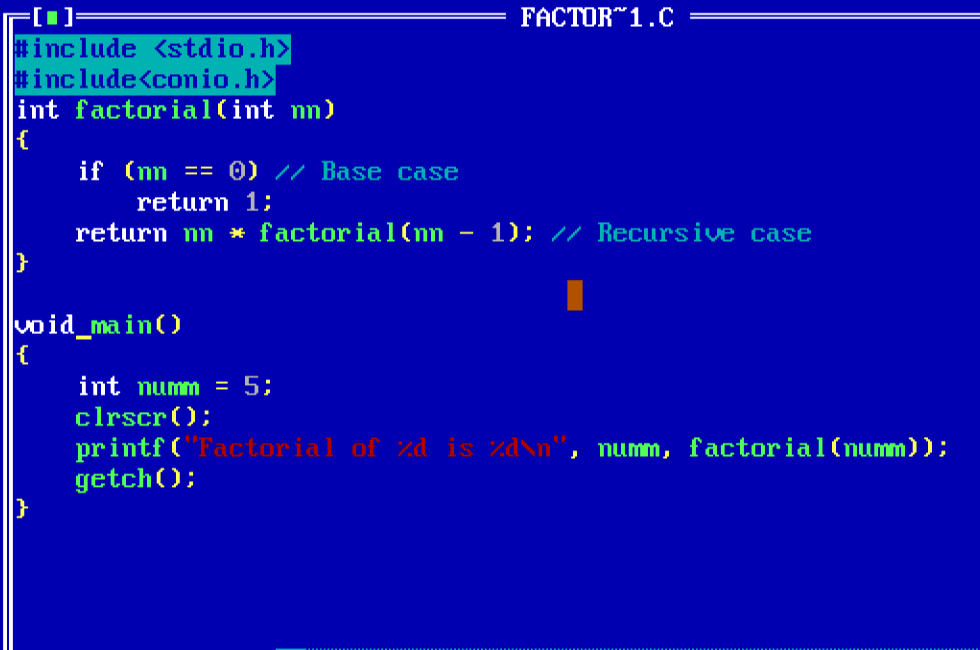
Simple Example: Factorial of a Number using Recursion
The factorial of nnn (n!n!n!) is defined as:
n!=n×(n−1)!
Base Case: 0!=10! = 10!=1
Code:
#include <stdio.h>
#include<conio.h>
int factorial(int nn)
{
if (nn == 0) // Base case
return 1;
return nn * factorial(nn – 1); // Recursive case
}
void main()
{
int numm = 5;
clrscr();
printf(“Factorial of %d is %d\n”, numm, factorial(numm));
getch();
}

Common Applications in Data Structures
1. Tree Traversal
Recursion is a natural fit for traversing(accessing each element) tree(hierarchical) structures:
- Pre-order Traversal: Process root, left subtree, right subtree.
- In-order Traversal: Process left subtree, root, right subtree.
- Post-order Traversal: Process left subtree, right subtree, root.
2. Linked List Operations
- Reversing a linked list using recursion.
- Searching(find an element) for an element in a linked list recursively.
3. Depth-First Search (DFS)
Recursion is commonly used in graph traversal algorithms like DFS, where visiting adjacent vertices recursively simplifies the logic.
Properties of Recursion in Data Structure
Recursion in C, especially in the context of data structures, is a powerful concept characterized by distinct properties. These properties are crucial for understanding how recursion works and how to implement it effectively.
1. Base Case
- Definition: A condition that stops further recursive calls.
- Importance: Prevents infinite recursion and ensures termination.
- Example: In calculating factorial, the base case is when n=0n = 0n=0, where the function returns 1.
if (n == 0) // Base case
return 1;
2. Recursive Case
- Definition: The portion of the function where the function calls itself to solve a smaller instance of the problem.
- Importance: Progressively reduces the problem size, moving towards the base case.
- Example: In factorial calculation, n!=n×(n−1)!n! = n \times (n-1)!n!=n×(n−1)! represents the recursive case.
return n * factorial(n – 1);
3. Divide-and-Conquer
- Definition: Recursion often follows the divide-and-conquer approach, where a problem is divided into smaller subproblems, solved recursively, and combined.
- Example: Merge sort divides the array into two halves(the left and right parts), sorts them recursively, and merges the results.
4. Problem Reduction
- Definition: In each recursive call, the problem size is reduced or transformed to move closer to the base case.
- Example: Traversing a linked list
void traverse(struct Node* head) {
if (head == NULL) // Base case
return;
printf(“%d “, head->data);
traverse(head->next); // Recursive case
}

